もう騙されない！偽情報の見分け方

突然ですが問題です

この薬は効果があると言えるか？

風邪薬Aが開発されました。この薬を風邪症状のある人100人に投与したところ、２日後には90人の人の風邪症状が改善されていました。

この薬は効果があると言えるでしょうか？

Yes / No

正解は・・・・「No」です（効果が無い　という意味でもありません）。

90人も治ったんだからYes!Yes!Yes!と答えてしまった人・・・騙される可能性があります。

非常に長い文章ではありますが、是非最後まで読んでいってください。

効果は比較検証するもの

なぜ風邪薬の効果はわからないのか？

前述の問いに対しての回答がわからないの理由を解説します。

「風邪薬が風邪を治したかわからないから」です。

どういうことかというと、風邪薬を投与しなくても風邪は治ったかもしれないですよね？

では、この薬が風邪に効果があるというためにはどのように確かめればいいのでしょうか？

比較しないとわからない

この風邪薬の効果を調べるには

✅風邪薬を投与した風邪症状のある100人

✅小麦粉の塊を投与した風邪症状のある100人

で比較検討する必要があります。

ちなみにそれぞれのグループを

「母集団」と言います。

この後も何度か出てくる言葉なので覚えておいてください。

比較してもわからない

さて、前章で"母集団を比較しなければならない"と書きましたが

母集団を比較しても「効果の有無」はわかりません。

「どっちやねん！」と思うかもしれませんが大事なことなので、最後までお付き合いください。

では何がわかるのでしょうか？

それは「２つの母集団の代表値の差」です。

はい、意味が分からないという人もブラウザバックしないでください。

一つずつ説明していきましょう。

代表値って何？

代表値とは母集団を代表する値のことです。有名どころだと

✅平均値

→母集団の合計値を足して、母集団のサンプル数で割った値です

✅中央値

→母集団のサンプルに順位をつけ、真ん中の順位のサンプルの値です

✅最頻値

→母集団のサンプルにおいて、最も出現する値です。

難しいので例題を出しましょう。

100m走のタイム比較

では例題として陸上部と帰宅部の100mのタイムを比較してみましょう。

（もちろんデータは架空ですよ）

✅平均値

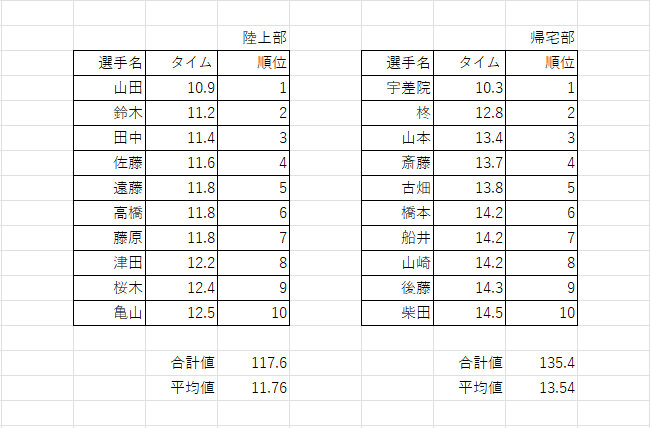平均は各選手のタイムの合計を選手の人数で割ります。

陸上部は11.76秒、帰宅部は13.54秒です。

✅中央値

母集団の中で順位をつけていき、真ん中の順位の人のタイムを採用します。陸上部では遠藤の11.8秒、帰宅部では古畑の13.8秒です。

リベ大動画で度々資産などに中央値が用いられるのは、データのばらつきが多いときに平均値よりも実態に近い値になるからです。

✅最頻値

一番多く出現する値です。

陸上部では11.8秒、帰宅部では14.2秒です。

タイムなどではあまり採用される値ではありませんが、類別変数の時に採用されます。変数の種類については今回は割愛します。

陸上部のほうが速いぞ！・・・とはならない

さて、代表値をいくつか挙げていったところで陸上部と帰宅部で差がありそうですよね？

陸上部は「平均値11.76秒」「中央値11.8秒」、帰宅部は「平均値13.54秒」「中央値13.8秒」だから陸上部のほうが速いぞ！という結論は導き出せません。

ではどうするのかというと単純な数値の比較ではなく、統計学的な検定を行って確定させます。検定にもいくつか種類があり、分散（データのばらつき）やサンプル数（選手の数）が重要なのですが、今回は割愛します。

"単純な数字の上下だけではわからない"と覚えておいてください。

統計学的な有意差とは？

さて、統計学で差を検定するわけなんですが、実は重要な前提条件があります。

「統計は否定しかできない」

ということです。じゃあどうやって、差が「ある」（肯定）って結論を出すの？という疑問がわきますよね。この疑問は直接解決できないので、ひねくれた方法で解決します。どのような方法かというと「差がないということを否定」することで「差がある」とします。この時に差がないという説を帰無仮説、差があるという説を対立仮説といいます。

だいぶややこしいかと思いますが、陸上部の場合の帰無仮説と対立仮説は下記のようになります。

帰無仮説＝陸上部と帰宅部には足の速さに違いは「ない」

この仮説を統計学的手法によって、否定することによって

対立仮説＝陸上部と帰宅部には足の速さに違いは「ない」とは「言えない」

　　　　→陸上部と帰宅部には足の速さに違いは「ある」とみなす

という結論を導きます。

傾向と個別事例について

表では宇差院は帰宅部なのに最速のタイムをたたき出しています。ですが"帰宅部のほうが陸上部よりも足が速い"という結論にはなりません。あくまでも、母集団同士を比較した際の差が傾向となります。

タバコを吸うと寿命が縮む傾向⇔世界最高齢者はタバコを吸っている

宝くじを買うと資産が減る傾向⇔宝くじで巨万の富を得た人がいる

このように一見すると逆のことを言っているようですが、成立する事項は存在するわけです。ある一つの属性で切り取った個別（サンプル）の集合が母集団なので、個別には当然例外（別の属性を保有している場合）が存在します。

例｜宇差院は全国レベルの強化選手であり、学校の陸上部ではなく県のクラブに所属している（学校では帰宅部扱いとなる）

個別事例なのか？母集団の傾向なのか？ここも情報精査時に間違えやすいポイントなので、見極める癖をつけましょう。

因果と相関の違い

さて、前項で差があるか否かの判定ができましたね。陸上部である＝足が速いという結果を得たときに陸上部と足の速さには「相関関係」があるといえます。しかし、「陸上部に入ると、トレーニングにより足が速くなる」という結論は導き出せるでしょうか？

答えはNoです。

何故ならば

✅足が速いから陸上部に入った

✅陸上部に入ったから足が速くなった

この２つのどちらかはわからないですよね？

陸上部のトレーニングの効果について結論を出したいならば、同じくらいの足の速さの人たちを用意して、陸上部のトレーニングを受けた人と何もしなかった人で比較するべきです。

その比較の結果を得て初めて、トレーニングの効果を証明することができます。この関係を「因果関係」といいます。

現実社会においては再現性を重視するのであれば、この因果関係を重視しなければなりません。だって、皆さんは結果を得るための行動を探していますもんね。相関があっても再現性があるとは限らないのです。

しかし世の中には相関関連から間違った因果関係を導いてしまうことが多々あります。この関係を疑似相関といいます。それでは、いくつかの疑似相関の例を見てみましょう。

例１.年賀状と年収

年賀状を出す人の年収＞年賀状を出さない人の年収

という傾向があります。ここに隠れている要素は「年齢」です。

年賀状を出す人のほうが比較的高齢であるため、賃金が年功序列の日本ではこのような相関が発生します。

というわけで年賀状を出したところで年収はアップしません。

例2.アイスクリームの売上と水難事故

アイスクリームの売上と水難事故の件数には相関があります。しかし、アイスクリームが売れる時期というのはいつ頃でしょうか？

そう、暑い時期ですね。暑い時期は水遊びが増えるので、水難事故も増えるわけです。ここに隠されている要素は「季節」ですね。

というわけでアイスの販売を減らしても水難事故は減少しません。

例３.朝ごはんとテストの点数

この例については私の個人的な見解が多分に含まれますのでご注意ください。朝ごはんを食べるとテストの点数が上がるという話を聞いたことがないでしょうか？私はこの相関には「家庭環境」という要素が隠されていると考えています。

朝ごはんを食べる子供というのは、朝ごはんが用意されている家庭で育つ子供です。つまり生活リズムが整っており、親が子供の面倒をよく見ている家庭ほど学力が高いのではないかと考えられます。

というわけで無理矢理、朝ご飯を食べさせてもテストの点数は良くならないと思います。

疑似相関を防ぐためには

このような実験を対照実験といいます。この実験設定の仕方がキチンとしているデータこそが信じられるデータと言えるでしょう。

冒頭に戻りまして風邪薬の例で言うと

✅風邪薬を投与した風邪症状のある100人

✅小麦粉の塊を投与した風邪症状のある100人

の２つのグループを用意するということですね。何故、小麦粉の塊を投与するかというと「薬をもらって飲んだ」という思い込みの力が風邪を治してしまうので、その影響を少なくするためです。

ここまでのまとめ

ここまで長かったですね。

もう一度振り返ると

「２つの母集団は差がないとは言えないから、差があるとみなすよ」

（ただし、疑似相関を防ぐために、トレーニング以外の要素は揃えておく）

「相関があり、ほかの要素は排除してるから、"陸上部のトレーニング→足が速くなる"とみなすよ」

ということで、

「陸上部でトレーニングをすると足が速くなる」

という"暫定の"結論に持って行きます。

はい、再び不穏な言葉が・・・”暫定”です。

ここからさらに突き詰めていきましょう

科学的定説とは？

科学は現状最も妥当な説を採用しているに過ぎない

いわゆるオカルトや似非科学などでは「現代科学では説明できない〇〇」などがありますが、当たり前です。

「説明できることを説明するのが科学（by 故・千石正一先生）」

暫定の結論一つ出すのに仮説・実験・棄却・検証を繰り返します。つまり昔からの人々の進歩の歩みなのです。

現在解決できないことの解決方法として、安易な解決方法を示すオカルトや似非科学などにすがってはいけません。

人生や真理に一発逆転ホームランなどないのです。

以下の本にも科学の本質が端的に記述されています。

科学とは常に反証の余地がなければならない

引用文献｜面白くて眠れなくなる進化論

宇宙人は将来見つかるかも？

宇宙人が「いないこと」を証明することは出来ません。一方で宇宙人が「いる」ことを証明するのは簡単です。連れてくればいいだけですからね。

存在しないことを証明する行為を「悪魔の証明」といい、立証することはほぼ不可能とされています。

現状の科学においては観測できる範囲では発見されていないために、宇宙人はいないとみなすのが妥当とされているわけです。

しかし、将来的に宇宙人が発見されれば、宇宙人はいないと考えるのが妥当という説から宇宙人は存在するという説が有力になりますよね。

前提は少ないほうがいい

オッカムのカミソリという言葉があります。なるべくシンプルに考えるべきという思考で進化学においても使用されています。とはいえ妥当性を高めるだけであり、絶対に正解とは言えません。

例えば進化学においては収斂進化はオッカムのカミソリに反しています。

参照HP｜Wikipedia

立場に注意しよう

発信者と受信者の立場

さて、ここまでの道のりについて来れましたか？

このような反証を繰り返して物事の真理というのは、ちょっとずつ見えてくるものなのです。

発信者というのは、ここまでの過程を意図的に省略、若しくはそもそも知らないです。

なぜ省略するのかというと、いちいちこんなことを話していては受信者が理解するのに手間取ってしまうからですね。とはいえ、ちゃんとした発信者というのはこの過程をたどってきています。それぞれの立場を考えると

発信者サイド｜なるべく情報を簡潔にまとめる

受信者サイド｜なるべく情報を複雑な角度から検討する

というように自分の立場に応じて使い分けてください。

こんなワードは要注意（投資編）

発信者は受信者に対して、「行動をさせる」のが目的です。とにかく行動させたいのですが、これ自体は特に悪いことではありません。問題は、受信者を行動させ、発信者のみが得をする場合ですね。いわゆるカモにしてくる場合です。今までの文章から抽出する内容はコレです。

「絶対は（基本的に）ない」

投資においては「確実」「ノーリスク」「元本保証」などのワードが出たら一回立ち止まりましょう。

特に「元本保証」は以下のように明確に法律で禁止されており、一考の余地すらございません。問答無用で切ってください。

この法律では銀行以外が不特定多数から資金を募り、元本を保証する行為は禁止されています。

こんなワードは要注意（商品系）

高価なブツについてはあまりにも単純化された「〇〇するだけ」「あの有名な○○も使っている（推薦している）」「有効成分○○が効く！」といった感じのワードは要注意です。検証においては複数の要素で成り立ちますので

「比較の仕方（比較する母集団の属性は妥当か？）」

「統計検証の有無（個別ではなく傾向で見ているか？）」

「サンプルの大きさ（十分な数で実験してるか？）」

「因果関係の明確さ（効果について妥当な論が展開されているか？）」

これらのことが読み取れなければ怪しんでください。

○○大学教授の〇〇が推薦などとあっても、金に目のくらんだ社会的地位の高い人物もたくさんいますので、信じ込まないようにしましょう。

まとめ

結論までは非常に長い道のり

さて、今回の説明は非常に長かったですよね。情報の受信時には疑って、更に疑うくらいがちょうどいいかもしれません。そのうえで妥当な結論だなと納得できれば自分の意見や行動に採用してもいいでしょう。大事なのは結論に至る過程なのです。発信者が「何故その結論に至ったのか？」に思いを馳せることができたら情報取得の精度は上がることでしょう。

✅統計的な比較検証を行っているか？

✅傾向と個別事例を混ぜていないか？

✅相関と因果を混ぜていないか？

✅因果について語っているか？

✅反証の余地はあるか？

✅「絶対」「確実」「ノーリスク」などの要注意ワードがないか？

このあたりを押さえておけば、良いでしょう。

とはいえ、疑いすぎて動けなくなるというのも弊害ですので、行動と情報収集のバランスを取りながら活動して行ってください。